5.6.3 The Multiply (Burn), Divide (Dodge), Screen, and Overlay Blending Modes
Multiply, Divide, Screen, and Overlay are all
multiplicative blending modes. The resulting pixel values are the
product or a function of the product of the foreground and background
pixels.
The actions of the Multiply and Screen modes on pixels
represented in the RGB cube are illustrated in
Figure
5.17.
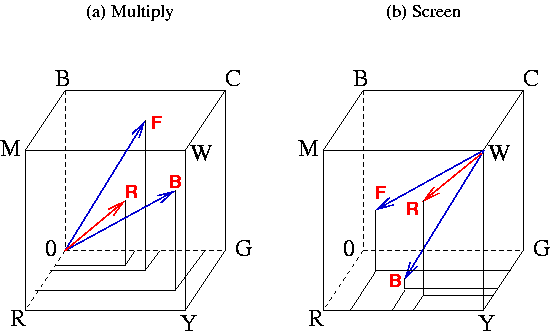
Figure 5.17:
The Multiply and Screen Modes in the RGB Cube
 |
For a foreground pixel whose position in the RGB cube is
[
r1,
g1,
b1] and a background pixel whose position is
[
r2,
g2,
b2], the resultant pixel for
Multiply mode is the
component-by-component product of the two, or
[
r1r2/255,
g1g2/255,
b1b2/255], where the division by 255 is
necessary to normalize the result back into the RGB cube. This can be
succinctly expressed by the equation
where the
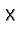
symbol means component-wise multiplication.
Due to the scale factor of 255, the component values of one RGB vector
are normalized to the range [0,1]. Thus, R is component-wise
smaller than either F or B. From previous discussions, you know
that smaller means darker because the projection onto the neutral axis
is closer to the origin. This is illustrated in
Figure
5.17(a) which shows two blue arrows
representing the foreground and background pixel positions and a red
arrow representing the component-wise product.
Figure
5.18(a)
Figure 5.18:
An Example of Multiply, Divide, Screen, and
Overlay Modes
 |
illustrates an example of applying
Multiply mode to the flower
image from Figure
5.15(a). As before, the
lower layer of this image is a uniform gray equal to
127
R 127
G
127
B. The result, shown in
Figure
5.18(a), is the image has been
made uniformly darker. In fact, because the lower layer is a medium
gray, the pixels values in the flower layer have been scaled by
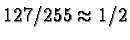
everywhere.
For a foreground pixel whose position in the RGB cube is
[r1,g1,b1] and a background pixel whose position is
[r2,g2,b2], you might imagine that the resultant pixel for the
Divide blending mode would be analogous to that for the Multiply mode. This would suggest something like
[255r2/r1,255g2/g1,255b2/b1]. However, this expression
presents two problems. The first problem is that when the foreground
pixel has a zero component, the result is not defined; the second
problem is that when the foreground pixel value is small, the result
can be so large that it is no longer inside the RGB cube. The first
problem is solved by adding one to each component of the foreground
pixel. This prevents a division by zero. The second problem is
solved by clipping values that are too large to the surface of the
cube.
A succinct expression for the Divide mode is
where
W is
255
R 255
G 255
B,
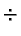
represents component-wise
division of two vectors, and
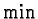
represents component-wise
minimization. Figure
5.18(b)
illustrates the application of
Divide to the flower image from
Figure
5.15(a). Here, you can see that some
parts of the resulting image are blown out to white. This occurs in
regions where the original flower image has small (that is dark) pixel
values. Note that
Divide always lightens an image because, it
divides each pixel component by a number less than 1.
The Screen blending mode has a lightening effect that is exactly
analogous to the darkening effect created by Multiply. This
concept is illustrated in Figure
5.17(b). As
shown in the figure Screen mode redefines the origin to be
255R 255G 255B, the white point in the cube. Thus, the vectors
to the foreground and background pixels are as shown by the two blue
arrows in Figure
5.17(b). Screen then
multiplies the two vectors, producing a resultant shown as a red arrow
in Figure
5.17(b). As with the Multiply
mode, the resulting vector of the Screen mode is shorter than
either the foreground or background vectors--but with respect to
the white point in the cube. Thus, the resulting vector is closer to
the white point, and, consequently, lighter than either the foreground
or background colors. The mathematical expression for Screen
mode is
Again, the factor of 255 is introduced to keep the resultant pixel
values inside the RGB cube.
Figure
5.18(c) illustrates an example of
applying the Screen mode to the flower image from
Figure
5.15(a). As predicted, the result is
everywhere brighter than in the original image of the flower. Also
notice that unlike Divide, Screen mode does not blow out
to white. Thus, although both Divide and Screen have
similar lightening characteristics, they have very different
personalities.
Finally, the Overlay mode is a combination of both Multiply and Screen. The equation for overlay mode is
where
Rs represents the resultant pixel value for
Screen mode
and
Rm represents that for
Multiply. This equation says that
the resultant pixel value for
Overlay mode is a combination of
the
Screen and
Multiply modes. The mix of the two modes
is proportional to the background pixel value.
Thus, if the background is dark (that is, has an RGB value close to
zero in all three components), the result of Multiply mode will
dominate and the result of Screen mode will be suppressed. The
opposite is true if the background pixel is light (that is, has an RGB
value close to white in all three components). Overall, Overlay
mode tends to make an image darker where it is already dark and
lighter where it is already light.
Figure
5.18(d) illustrates an example of
applying Overlay mode to the flower image from
Figure
5.15(a).
